Brutalno rešavanje robota
Ovo je kratak primer optimizacije brutal-force pristupa korišćenog za rešavanje logičkog problema - igrice “Little Broken Robots”.
Izazov je napisati program koji rešava logičke probleme. S vremena na vreme, koliko već ono dopušta, dohvatim neku simpatičnu logički igricu i pokušam da je rešim programski. To je drugačija vrsta programiranja, koja se ne sreće svaki dan u praksi.
Problem
Tabla sa poljima sadrži izvestan broj tokena. Svaki token je označen brojem, koji predstavlja koliko polja on može da “pokrije”. Cilj igrice je da se pokrije cela tabla, tako da se iskoristi svaki token, a da ne ostane ni jedno slobodno polje. Naravno, putanje tokena se ne mogu preklapati. Ponekada tabla sadrži polja koja moraju da se ignorišu.
Primer jednog problema:

i korak do njegovog rešenja:
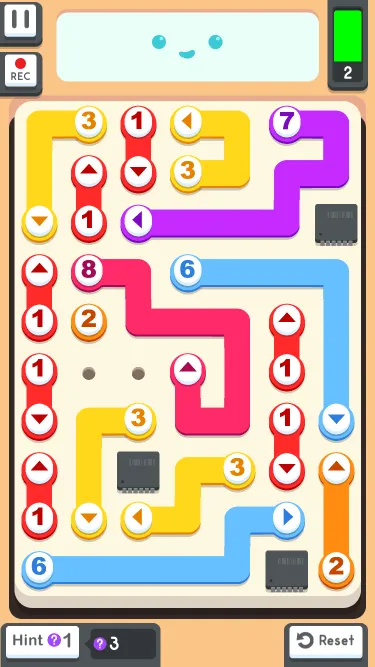
Ideja rešenja
Najprostiji pristup je brtual-force, prosto korišćenje siline jačine kompjutera da proba sve mogućnosti i nađe rešenje. Rešenje delim na dva algoritma:
1. Odredi sve putanje za svaki token
Prvi korak je da za svaki token odredim sve moguće putanje:
10. započni drvo
20. za svaki list idi: GORE, DOLE, LEVO, DESNO
30. ukloni preklapanja putanje sa samom sobom
40. GOTO 202. Iscrtaj putanje za sve tokene
A zatim:
10. za svaki token iscrtaj jednu putanju
20. ako se putanje preklapaju na tabli, GOTO 10
30. ako ima slobodnog polja, GOTO 10
40. rešenjePrimena algoritma
Da bi uopšte imao ideju koliko ima mogućnosti, programom se lako dolazi do toga da je broj mogućih putanja za token vrednosti 8 koje se ne preklapaju 5916 (algoritam #1). Na polju koji ima 3 tokena, iteracija svih putanja (algortam #2) izgleda ovako:
T1 | T2 | T3
--------------
1 1 1
1 1 2
...
1 1 5916
1 2 1
1 2 2
...
2 1 1
...Koji trenutka kasnije, program izbaci ispravno rešenje.
Skaliranje
Ok, hajde sada da primenim algoritam na primer sa početka teksta, u kome ima značajno više tokena u igri. Trebaće samo malo više vremena da se dođe do rešenja, zar ne?
Da. Malo više. Kao u… “nikada”. Jer je broj iteracija ovoliki:
30979159172252806466764800tj. negde oko 3 * 10^26. Neće da može.
Optimizacija #1
Očigledno, nema smisla da crtam baš sve moguće putanje za svaki token. Algoritam #2 se može unaprediti tako da odbaci sve putanje koje nisu validne:
- koje izlaze van table,
- koje prelaze preko zabranjenog polja
Drugim rečima, da iscrtam sve putanje koje mogu da stanu na tablu, a da potom detektujem da li se one preklapaju.
Klik-klak, unosim izmenu, pokrenem kod i… opet čekam. Ovaj put bih možda i za života dočekao rešenje jer je broj kombinacija sledeći:
736394232420000tj. 7.3 * 10^15. Značajno manje, ali i dalje puno - toliko da računar ne uspava da pronađe rešenje u razumno kratkom roku.
Optimizacija #2
Potrebno je još optimizacije algoritma #2. Umesto da crtam sve validne putanje za svaki token, pa onda radim proveru ispravnosti rešenja; sada odmah radim detekciju validnosti putanje dok se ona iscrtava:
10. uzimi token
20. iscrtaj jednu njegovu putanju
30. putanja nije validna? uzmi sledeću putanju tokena; GOTO 20
40. putanja je validna? idi na sledeći token; GOTO 20Ovim simuliram zapravo kako bi i čovek sam to radio: mi ne bi crtali sve putanje, već samo validne, koje se ne preklapaju.
Još jedna optimizacija je ovde moguća - ukoliko krenem od tokena sa većim brojem, time u startu pokrivam više polja table, pa se ranije detektuju preklopljenje putanje.
Ove optimizacije daju sledeći broj prolaza:
108774113što je reda veličine 10^9 - e to je već nešto što računar može da reši za dovoljno kratko vreme.
Zaključak
Iskreno, nema ovde nešto pametno zaključiti. Optimizacijama se dovijamo da smanjimo broj iteracija.