Monad

2. oktobar 2023.

Iz beležnice programera: dal’ se kaže oštro “Monad” ili pak “Monada”, još onako razvučeno, po vojvođanski, uz štrudlu sa makom?

Ovo je nekakav pregled pojmova iz teorije kategorija primenjenih na programske jezike (funkcionalno programiranje) potrebnih da se razume šta je monad. Postoji puno sličnih sadržaja; nadam se da ovim donosim jedan praktičan pogled. Voleo bih da znam više, ali tako je - kako je; i ovo malo možda bude od pomoći, pa makar i ne bilo sve tačno.

Monad je apstrakcija kompozicija funkcija. Zato ima smisla razumeti njegovu definiciju:

Monad je monoid u kategoriji endofunktora.

Teorija kategorija je generalna teorija koja se najviše bavi relacijama, tj. odnosima između objekata. Reč je o apstraktnoj, tkzv. “čistoj” matematici: ne zanimaju nas konkretni brojevi, već relacije, odnosi, relacije relacija… Takvo apstraktno razmišljanje je našlo primenu u raznim granama nauke. A gde je apstrakcija, eto mesta za filozofiju :)

Legenda:

⭐️ - objašnjenje koncepta, pojma i sl.
🤦‍♂️ - dopunski deo za štrebere koji izlazi van teme.
🔥 - laičko objašnjenje. Nikakva formalna definicija, a često ni tačna; ali je meni pomoglo.

Kategorija

⭐️ Skup je kolekcija različitih stvari, koji se nazivaju elementi skupa. Elementi skupa mogu biti bilo šta. Skup može biti prazan. Elementi skupa mogu biti i drugi skupovi.

⭐️ Algebarska struktura je skup koga čine:

jedan ili više elemenata,
operacije nad elementima, tipično binarne,
konačan broj posebnih elemenata koji se nazivaju identitet.

Takav neprazan skup je, praktično, algebarska struktura; kao i sve ostale kasnije navedene.

⭐️ Kategorija je algebarska struktura koju čine objekti i morfizmi. Pored toga, u kategoriji vladaju dva zakona.

⭐️ Objekti kategorije mogu biti šta god, postojeće ili zamišljeno: brojevi, avioni, kamioni, cveće, skupovi, matrice.

⚠️ Objekti iz teorije kategorija nisu u vezi sa OOP, samo dele isto ime. Zaboravimo na objekte iz OOP! Amen.

⭐️ Morfizmi su relacije između objekata. Morfizmi se nazivaju i “strelicama” (engl.: arrow). Morfizam je mapiranje između dva objekta kategorije. Nemaju svi parovi objekata kategorije morfizam između njih.

Ako su A i B objekti iz kategorije C, onda se njihova relacija, tj. morfizam f piše kao:

f: A → B

🔥 Teorija kategorija se više bavi morfizmima nego objektima!

⭐️ Kompozicija. Za kategoriju nije dovoljno da samo postoje relacije, tj. morfizmi. Da bi se formirala kategorija, mora postojati način kompozicije morfizama.

Kompozicija se označava kružićem ∘ koji se čita: “posle”. Za svaki par morfizama f:A→B i g:B→C, mora postojati morfizam h koji je njihova kompozicija i povezuje A i C:

h = g ∘ f : A → C

Kažemo da je f u kompoziciji sa g; čitamo da je g posle f.

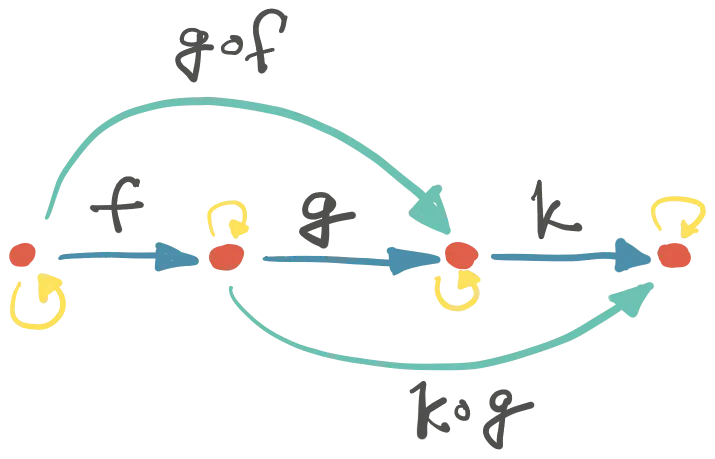
Dakle, ne samo da moraju postojati odnosi (relacije, funkcije, morfizmi, strelice) između objekata kategorije, nego moraju biti takvi da se svaki par povezanih morfizma može zameniti jednim morfizmom koji je njihova kompozicija.

Kompozicija ∘ je binarna operacija dva morfizma.

⭐️ Zakoni kategorije. Opisanom kompozicijom morfizama vladaju dva zakona (dve aksiome). To su pravila koja operacije u algebarskoj strukturi moraju da poštuju.

⭐️ Zakon identiteta: za svaki objekat u kategoriji mora postojati morfizam identiteta (ili samo, identitet.)

Identitet je morfizam koji preslikava objekat u samog sebe. Za svaki objekat A u kategoriji mora da postoji identitet morfizam: id/A:A→A takav da:

id/A ∘ f = f = f ∘ id/A

Kako god kombinovali morfizam sa identitetom, morfizam se ne menja.

Ovo je način da se predstavi “nula” kompozicije, tj. operacija koja ne radi ništa. (Kao što je to slučaj sa, na pr., nulom i sabiranjem.)

⭐️ Zakon asocijacije: kompozicije su asocijativne. Za svaka tri morfizma f, g, i h važi:

h ∘ g ∘ f = (h ∘ g) ∘ f = h ∘ (g ∘ f)

Kojim god redom da izvršavamo kompoziciju ∘, rezultat ostaje isti. Zato nam zagrade nisu neophodne i izostavljaju se u pisanju.

🚀 Sada je kategorija potpuno definisana.

Kategorija: sažetak

⭐️ Klasa u matematici je kolekcija skupova koji se svaki jedinstveno može odrediti nekom osobinom koju dele svi članovi tog skupa. Skup {2, Plavo} ne može da pripada klasi. Skupovi {2,8} i {Plavo, Crveno, Žuto} bi mogli da čine jednu klasu.

🤦‍♂️ Sumiramo: u kategoriji C se nalaze:

objekti - koji pripadaju klasi ob(C).
morfizmi - koji pripadaju klasi hom(C). Kada se napiše hom(A,B) to označava hom klasu svih morfizama od A do B.
Binarna operacija ∘ koja se naziva “kompozicija morfizama”, koja za svaka tri objekta A, B i C imamo definisano:

∘: hom(B,C) x hom(A,B) → hom(A,C)

Ova binarna operacija se još pokorava zakonima: asocijativnost i identitet.

Primer kategorije: WWW

Da li su internet stranice (WWW) kategorija?

objekti su stranice ✅
morfizmi su linkovi; strana A ima link ka strani B ✅
da li postoji kompozicija? Ako A linkuje na B, B na stranu C, da li postoji link A na C? Ne. ❌

Internet stranice (WWW) nisu kategorija. Da generalizujemo: bilo koji graf nije kategorija.

Međutim, ako promenimo šta je morfizam u WWW grafu, stvari se menjaju. Ako morfizam: “direktan link” zamenimo sa “putanjom” (koju čine 0..N linkova), stvari postaju drugačije. Putanja je prosto mogućnost da se sa stranice A linkovima dođe na stranicu B. Tada WWW zapravo postaje kategorija:

postoji kompozicija: ako postoji putanja od A do B i od B do C, onda postoji putanja od A do C. ✅
identitet postoji: putanja do samog sebe. ✅
asocijativnost je na mestu. ✅

⭐️ Ovakva kategorija se naziva i slobodnom (“free category”), jer se konstruiše nad slobodnim spajanjem linija direktnog grafa, tj. nad putanjama.

Primer kategorije: Nasleđivanje programskih tipova

Hajde da definišemo kategoriju nad tipovima u programu:

objekti su tipovi u programskom jeziku: Int, String, Book… ✅
morfizam je relacija “isSubclass”. Na primer, Int > Number. ✅
kompozicija: postoji. Primer: Int > Number > Object ✅

Tipovi u programskom jeziku čine kategoriju.

Kratko o tipovima u programskom jeziku

Tip u programskom jeziku određuje skup svih mogućih vrednosti koje su tog tipa. Na primer, Bool je skup dve vrednosti. Number predstavlja skup svih mogućih brojeva koji se mogu predstaviti u programskom jeziku. Ovaj skup uključuje i Int, koji je podskup samo celih brojeva.

I funkcije u programskom jeziku imaju tip. Tip String→Int je skup svih mogućih parova vrednosti String, Int (bez obzira šta funkcija konkretno radi.)

Tipovi u programskom jeziku zato mogu da tvore klasu u teoriji kategorija.

🔥 Tipovi u programskom jeziku su samo vrednosti. Zato se mogu kombinovati. Zato kada je funkcija “first-class citizen”, ona predstavlja takođe vrednost.

Kategorije u programiranju: Scal/Hask

Pokazalo se da se kategorija može oformiti i u programskom jeziku. Svaki programski jezik ima svoju kategoriju. Tako se u Haskelu takva kategorija naziva “Hask”, u Skali “Scal”.

Objekti kategorije programskog jezika čine svi tipovi tog jezika. Na primer: Int, String, Book; ali i List[Book], Map[Int, Double].

Morfizmi odgovaraju funkcijama. Morfizam f je funkcija koja prima objekat (tip) A i vraća objekat (tip) B:

def f(a: A): B

Morfizmi takođe imaju tip u programskom jeziku, na pr. (A):B.

Kompozicija postoji:

def f(a: A):B
def g(b: B):C
def h(a: A):C = g(f(A))

Asocijativnost takođe radi.

Morfizam identiteta je funkcija koja vraća nepromenjenu ulaznu vrednost:

def identity(a: A):A = a

🚀 Kategorija programskog jezika je time definisana.

Dva sveta

🔥 Programske strukture koje slede su nekakvi kontejneri vrednosti.

Sve objekte iz kategorije programskog jezika (dakle, sve tipove) možemo podeliti u dve celine:

u jednoj su “obični” tipovi: Int, Book.
u drugoj su tipovi koji sadrže druge, kontejneri: List[Int], Option[Book], itd.

Kontejner nosi vrednost(i). Kontejner je kutija u koju stavljamo vrednost. Kontejner je nekakav kontekst za vrednosti koje nosi. Najvažnije, kontejnera ne zanima šta sadrži, šta to nosi. Zanima ga samo mogućnost da primenjuje morfizme na sadržaj. Zato su nam kontejneri interesantni.

(Šredinger je stavio mačku u kutiju Maybe :)

Nije dovoljno da samo primenjujemo funkcije (morfizme) na sadržaj kontejnera. Neophodno je da te kontejnere takođe nekako kombinujemo. Zato kontejner mora da ima odgovarajuće ponašanje, tj. interfejs. Nadalje pričamo o tome.

Kontejner u programskom jeziku možemo uopšteno označiti i ovako: F[_].

Funktor

⭐️ Funktor je funkcija koja preslikava jednu kategoriju (algebarsku strukturu) u drugu i održava njenu strukturu. Za dve kategorije C i D, funktor je funkcija F:C→D koja:

preslikava sve objekte iz C u D
preslikava sve morfizme iz C u D
održava kompoziciju: F(g ∘ f) = F(g) ∘ F(f)
održava identitet: F(id/A) = id/F(A)

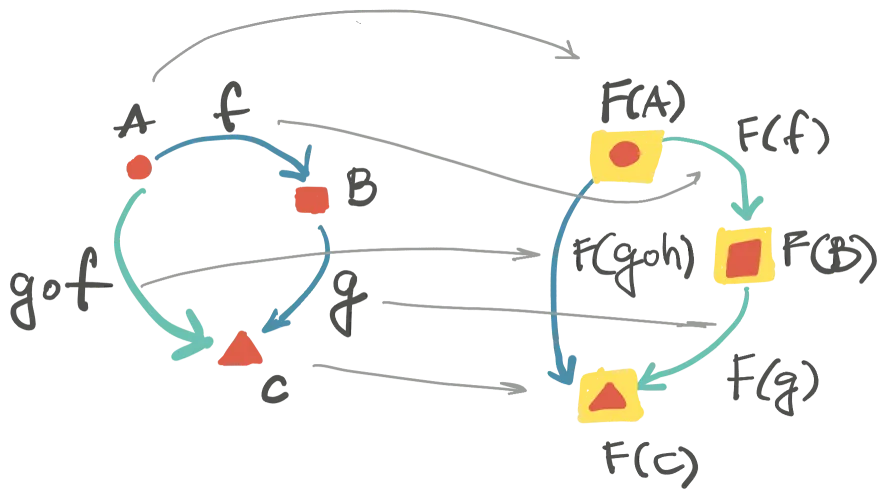
🤦‍♂️ Kovarijant funktor označava smer C→D. Postoji i kontravarijant funktor od tkzv. “obrnute kategorije” ka D. Primetite nazive: da li podsećaju na generičke parametre u programiranju?

⭐️ Endofunktor. Kategorije C i D ne moraju biti različite: funktor može da preslikava kategoriju u samu sebe. Takav funktor se naziva endofunktor. Za funktor se kaže da je homomorfizam kategorije (jer održava njenu strukturu.)

U kategoriji programskog jezika svi funktori su ujedno endofunktori; preslikavaju kategoriju samu u sebe.

Funktor u programiranju

⭐️ Type constructor je generička definicija programskog tipa. List nije tip, ali List[String] jeste tip. List je konstruktor tipova; obeležava se List[_]. Konstruktor tipa je ujedno i funkcija, jer A→List[A].

Opšti konstruktor tipa se može zapisati i kao: F[_].

⭐️ U programiranju funktor je konstruktor tipova koji zadovoljavaju određeni kriterijum. Tip koji funktor konstruiše kao konstruktor tipova, dakle, mora da implementira map/fmap funkciju, koja radi preslikavanje sadržaja.

Ukratko:

funktor (konstruktor tipova) preslikava A u F[A].
F[A] implementira map() koji preslikava sadržaj, na pr. iz F[A] u F[B].
zadržane su osobine kompozicije i identitet.

⭐️ Funkcija map(f:A→B) primenjuje morfizam na vrednost koju funktor nosi. Funkcija map() “podiže” (engl.: lift) morfizam iz “običnog” sveta u svet “kontejnera” i primenjuje ga na vrednost u kontejneru.

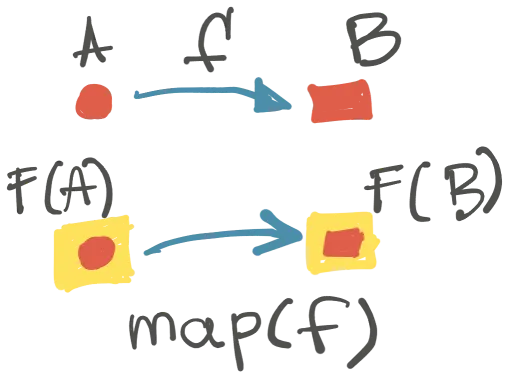
Funkcija map(f) je takođe morfizam za funktore.

⭐️ Kako izgleda Functor trait u Skali:

trait Functor[F[_]] {
  def map[A, B](fa: F[A])(f: A => B): F[B]
}

🤦‍♂️ F je ujedno i efekat (ili kontekst). List je, dakle, i funktor i efekat. Efekat ne mora da bude funktor.

Efekat služi da se apstrahuje različito ponašanje. Tako efekat Option enkapsulira baratanje sa nepostojećim vrednostima.

Da se podsetimo: List nije tip. List[String] je tip, ali više nije funktor (nema konstruktor tipova).

🔥 Sažetak. Funktor je konstruktor tipova koji su kontejner, nose vrednost. Tip koji funktor pravi ima map() kojom podiže funkciju iz kategorije u svoj svet. map() primenjuje funkciju na vrednost koju kontejner sadrži, čime je menja.

Monoid

⭐️ Polugrupa je neprazan skup (algebarska struktura) koji ima asocijativnu binarnu operaciju * (oznaka, nije množenje). Operacija * vraća elemenat iz istog skupa.

⭐️ Monoid je polugrupa koja još ima element identiteta id, koji za svaki element iz grupe x zadovoljava:

id * x = x * id = x

id je jedinični element koji u binarnoj operaciji sa bilo kojim drugim elementom iz polugrupe vraća taj element neizmenjen.

🤦‍♂️ Monoid je takođe kategorija (wtf:). Monoid kao kategorija ima samo jedan objekat - pomenuti skup elemenata. Morfizmi u toj kategoriji su binarne operacije. Ona preslikavaju skup u samog sebe.

Svaka binarna operacija u skupu je ujedno i morfizam za taj skup. 2 + 5 postaje 2.add(5). Morfizam add(5) preslikava skup u sebe samog (2 u 7.)

⭐️ Monoid je apstrakcija kombinovanja dva elementa skupa.

Zahvaljujući asocijativnosti, ovakva apstrakcija dozvoljava, na primer, paralelno izvršavanje operacije * nad skupom. Na primer, u monoidu sa celim brojevima 1, 2, 3 i 4, možemo u isto vreme (paralelno) kombinovati prvi par (1+2=3) i drugi par (3+4=7), a potom rezultate (3+7).

Monoid dozvoljava “divide-and-conquer” strategiju, inkrementalnu akumulaciju, paralelizam…

Monoid u programiranju

⭐️ U programiranju monoid je tip (dakle, skup) koji implementira funkciju foldLeft/reduce.

def foldLeft[B](z: B)(op: (B, A) ? B): B

Fold je binarna operacija koja kombinuje dve vrednosti u jednu. Da bi se tako nešto primenilo na, recimo, List[Int] treba nam i početna, nulta vrednost. Kada su u pitanju brojevi, to je obično 0 (za operaciju sabiranja) ili 1 (za operaciju množenja). Ova vrednost je identitet id.

Monoid ne mora da sadrži samo iste tipove. Rekli smo da je monoid skup (što je vrlo širok pojam); element mogu biti i, na pr.: Int i String.

⭐️ Monoid se formalno zapisuje kao triplet: (S, *, id): skup elemenata, operacija, identitet.

Primeri monoida:

(Int, +, 0)
(Int, *, 1)
(String, +, "")

⭐️ Monoid u programiranju je tip koji sadrži binarnu asocijativnu funkciju i element identiteta.

🔥 Sažetak. Monoid je struktura, kontejner koji ima implementiranu funkciju za kombinovanje dve vrednost (foldLeft); ta implementacija mora da definiše i nulti-element za kombinovanje (tkzv. identitet).

Prirodne transformacije

Vratimo se kratko nazad. Počeli smo sa kategorijom objekata koji se mapiraju jedan na drugi. Funktor je dao mogućnost preslikavanja celih kategorija. Postoji sledeći, viši nivo apstrakcije: mapiranje funktora. Dakle:

strelice/morfizmi preslikavaju objekte jedan u drugi unutar kategorije.
funktori preslikavaju cele kategorije.
prirodne transformacije preslikavaju funktore.

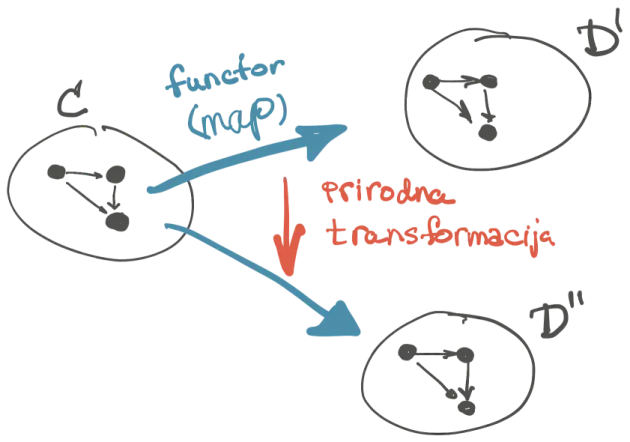
Primer prirodne transformacije: metoda head() na List[T] vraća Option[T]. Reč je dakle o morfizmu: List[T]→Option[T].

⭐️ Prirodne transformacije su morfizmi za funktore (relacija za relacije) koji čuvaju unutrašnju strukturu. Da li to izgleda da možemo da napravimo kategoriju endofunktora?

Monad (korak #1)

⭐️ Monad se definiše kao triplet M = (F, unit, flatMap).

F je skup elemenata endofunktora: F:C→C
unit je prirodna transformacija od identiti funktora Id:C→C na naš funktor F. Dakle: unit:Id→F. Ona “upakuje”, podiže vrednost u monad.
flatMap je prirodna transformacija: T∘T→T. Ovde je T∘T kompozicija endofunktora; kontejner u kontejneru. flatMap zna da otpakuje ugnježdene strukture. Ona time dozvoljava ulančavanje monada.

Da li ova definicija podseća na monoid? To je zato što monad i jeste monoid.

Monad (korak #2)

⭐️ Ako je C bila kategorija tipova, neka je End(C) kategorija endofunktora:

objekti: endofunktori. ✅
morfizmi su prirodne transformacije endofunktora. ✅
kompozicije prirodnih transformacije postoji. Nisam baš razumeo kako, ali kapiram da se sposobnost kompozicije prenosi usled očuvanja struktura. ✅
identit endofunktor: unit/lift/pure. ✅

Bitno je da elementi monade (endofunktori) čine kategoriju da bi mogli da ih kombinujemo.

🚀 Monada je monoid u kategoriji endofunktora. Monoid nam donosi pakovanje vrednosti i otpakovanje ugnježdenih struktura, funktor nam donosi uvezivanje monada.

Monad u programiranju

🔥 Slično funktoru, monad je konstruktor tipova, kontejnera za vrednost, koji zadovoljavaju određeni kriterijum. Tipovi (kontejneri) koje monad kreira moraju da implementiraju flatMap() i unit() funkcije.

Primer:

// naš objekat kategorije
class User(name: String) {
  override def toString(): String = "<" + name + ">"
}

// dobavlja korisnika
def fetchUser(id: Int): Option[User] =
  if (id == 2) None else Some(User("user" + id))

// kompozicija
val users = List(1,2,3).map(id => getUser(id))

Rezultat je List[Option[User]] sa 3 elementa, kontejneri u kontejneru. To nije ono što želimo.

Potrebno je da transformišemo kontejner List tako što ćemo kombinovati elemente i otpakovati ugnježdene kontejnere.

⭐️ Funkcija flatMap() radi upravo to - mapira, pa potom “izravnjava” (ispravlja) sadržaj kontejnera:

val users = List(1,2,3).flatMap(id => getUser(id))

Rezultat je List[User] sa 2 elementa.

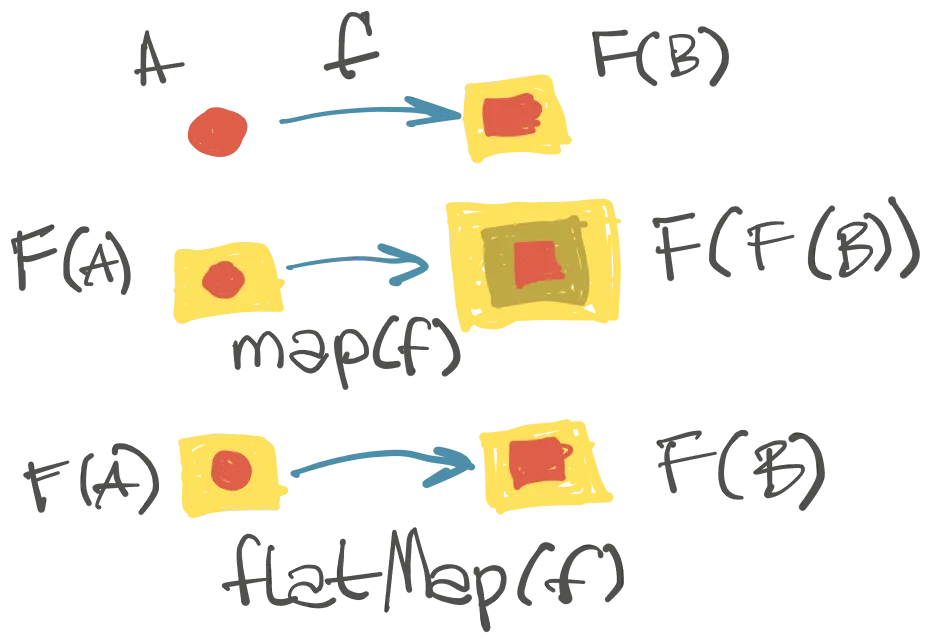
Funkcija flatMap() pretvara F[F[_]] u F[_].
Funkcija unit() “podiže” vrednost u kontejner monade: A→M[A].

⭐️ Monad u Skali može da izgleda ovako:

trait Monad[M[_]] {
  def unit[A](a: => A): M[A]
  def flatMap[A,B](ma: M[A])(f: A => M[B]): M[B]
}

Ovde je M monad, konstruktor tipa koji implementira flatMap i unit. U govoru često izjednačavamo tip koji monad kreira sa pojmom “monad” (slično je i sa funktorom.) Drugim rečima, često za sam kontejner kažemo da je monad.

⭐️ Monad je ujedno i funktor. Zanimljivo da metodu map funktora možemo da dobijemo kao:

def map[A, B](ma: M[A])(f: A => B): M[B] =
  flatMap(ma)(x => unit(f(x)))

Šta se dešava? Izvršimo mapiranje ulaza f(x), ali kako vrednost nije u kontejneru moramo je “podići” sa unit(). Ovu kompoziciju definišemo kao funkciju, koja je sada argument za flatMap. flatMap() radi samo sa funkcijama koje podižu vrednost u kontejner.

Trivija za kraj

Ime “monad” je spoj “monoid” i “triad”: “monoid” jer je monoid u kategoriji endofunktora, “triad” jer pakuje tri stvari: endofunktor sa dve prirodne transformacije.

Obećao sam filozofiju: teorija kategorija se ne bavi mnogo vrednostima. Može se doći do shvatanja da nije važna vrednost objekta, već da je objekat definisan samo svojim relacijama. Da ponovim: nešto je definisano samo svojim relacijama, a ne onime što zapravo jeste! To govori Yoneda lema. Da li to znači da je postojanje bilo čega jednoznačno definisano samo postojećim relacijama?

(Kog sam andraka sve ovo i pisao…) Idemo dalje.